• Lecture 1:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• Brief review of basic notions (groups, rings, and fields)
• Some examples
• Homomorphisms, examples
• Equivalence relations and equivalence classes.
• Examples: congruence (clock arithmetic)
• Integral domains, ideals
• Division Algorithm (with proof) for $R[X]$ when $R$ is a commutative ring and the divisor is monic. Note over a field any non-zero polynomial can be made monic by multiplying by a constant.
• Division algorithm for $\mathbb{Z}$.
• Consequences of the division algorithm: $F[X]$ is a principal ideal domain (PID) if $F$ is a field. $\mathbb{Z}$ is a PID.
• Example using the division algorithm for polynomials.
• We passed out the following stuff:

1. You are encouraged to discuss problems with each other and to ask the instructors and tutors questions about them, but hand in your own version of the solution. Your write-up should be done entirely on your own.
2. You are discouraged from browsing the internet for solutions to problems.
3. Please ask questions of the teacher in class.
4. Please don't talk in class, and please put your cell phones away. But, once again, do ask questions. If something seems unclear please let us know.

Solutions are due on 10^th May, 2018 at the beginning of class. This will not count toward your course grade. Roger and Sylvia will make comments on papers and return them to students on 11^th May, 2018 (maybe).

1. If $G$ is a group with identity element $1$ such that $x^2=1$ for every $x\in G$, prove that $G$ is abelian.
2. If $R$ is a ring such that $x^2=x$ for every $x\in R $, prove
   1. $2x= 0$ for every $x\in R$, and
   2. $R$ is commutative.
3. Factor the polynomial $x^3+2x-1$ over the field $F$ completely (into a product of irreducible polynomials that you justify are irreducible).
   1. If $F=\mathbb{Q},$ the rational numbers.
   2. If $F=\mathbb{C}$, the complex numbers.
   3. $F=\mathbb{F}_5=\mathbb{Z}/5\mathbb{Z}$, the field of integers mod $5$.

• Lecture 2:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• We asked students to read pages 6--13 in Milne (up through Remark 1.18) and learn the Euclidean Algorithm (1.8) for finding the GCD of two polynomials and expressing it as a linear combination of the two polynomials.
• Reminders concerning rings, fields, PIDs.
• Definition of ring homomorphism.
• $\mathbb{Z} \times \{0\}$ is an ideal of the ring $\mathbb{Z} \times \mathbb{Z}$. It's actually a ring with identity $(1,0)$, but it's not a subring of $\mathbb{Z}\times\mathbb{Z}$, since its identity is not the same. (The identity element of $\mathbb{Z}\times\mathbb{Z}$ is $(1,1)$.)
• A field $F$ has exactly two ideals, namely, $\{0\}$ and $F$. A commutative ring with exactly two ideals is a field.
• Field homomorphisms are always injective (one-to-one).
• Fields are integral domains.
• A finite integral domain is a field. (Proof: Let $a$ be an arbitrary non-zero element of the finite integral domain $R$. We have to show $a$ has an inverse in $R$. Look at the powers: $a, a^2, a^3, a^4, \dots$. They can't all be distinct (since $R$ is finite), so say $a^i = a^j$, with $i < j$. Then $a^i \cdot 1 = a^i = a^j = a^i \cdot a^{j-i}$. By cancellation (Milne's definition of ``domain"), we have $a^{j-i} = 1$. Since $j-i-1\ge 0$ we can set $b=a^{j-i-1}$ and get $ab = 1$.)
• If $p$ is a prime number, then $\mathbb{Z}/p\mathbb{Z}$ is a field with $p$ elements, often denoted $\mathbf F_p$.
• The {\it prime subfield} of a field $F$ is the smallest subfield of $F$. It's isomorphic either to some $\mathbb F_p$ (if the characteristic is $p$) or to $\mathbb{Q}$ (if the characteristic is $0$).
• Defined irreducible element of a domain (not a unit, and every factorization involves a unit).
• For a field $F$, units of $F[X]$ are the polynomials of degree $0$ (non-zero constant polynomials).
• For a field $F$ a polynomial $f(X)$ is irreducible in $F[X]$ if and only if it cannot be written as a product of two polynomials of lower degree.
• Be careful: $2X^2+2$ is irreducible in $\mathbb{Q}[X]$ but not in $\mathbb{Z}[X]$.
• A consequence of the Division Algorithm: Let $F$ be a field, $f(X)$ a polynomial in $F[X]$, and $c$ an element of $F$. Then $X-c \mid f(X) \iff f(c)=0$. A further consequence: If $f(X)$ has degree $2$ or $3$, then $f(X)$ is irreducible if and only if $f(X)$ has no roots in $F$. But this fails for degrees bigger than $3$. For example, $X^4+2X^2 +1$ has no roots in $\mathbb{Q}$; but it's certainly not irreducible in $\mathbb{Q}[X]$, since $X^4+2X^2+1 = (X^2+1)^2$.

• Lecture 3:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• In a PID, if $a\mid bc$ and $a$ and $b$ are relatively prime (have GCD = 1), then $a\mid c$ (Sometimes called Euclid's Lemma , related to [Book 1.9].) (We proved this assuming the Euclidean Algorithm, that is, the GCD of two things is a linear combination of the two things, related to [Book 1.8].) We also used:
• The Two-out-of-Three Lemma: In a commutative ring, if $a\pm b=c$ and two of $a,b,c$ are divisible by some element $r$, then so is the third. Related to [Book 1.9].) (We proved one of the six cases, leaving the rest to the students' imagination and amusement.)
• Impossible Rational Roots Theorem (Proposition 1.11 in book): Let $f(X)\in \mathbb{Z}[X]$ and let $r\in \mathbb{Q}$ be a root of $f(X)$. If $r = \frac{m}{n}$ in lowest terms (that is, $m$ and $n$ are relatively prime integers), then $m$ divides the constant term of $f(X)$ and $n$ divides the leading coefficient. This cuts the search for roots down to a finite problem. In particular, if $f(X)$ is monic, to test for rational roots you need only try (positive and negative) divisors of the constant term. This is particularly useful for determining whether or not a cubic polynomial is irreducible in $\mathbb{Q}[X]$. (Some people call this the Possible Rational Roots Theorem . Question: Is $1$ a possible rational root of $X^2+1$?
• We gave a detailed proof of the Impossible Rational Roots Theorem and discussed Eisenstein's Criterion [Book 1.16]), without giving the proof. Warning: Many polynomials are not Eisensteinable. If there is no prime satisfying the requirements of Eisenstein's Criterion, the test is inconconclusive: the polynomial may or may not be irreducible; use another approach. (For example, consider $X^2+1$ and $X^2-1$.)
• In trying to determine whether or not a polynomial $f(X) \in \mathbb{Q}[X]$ is irreducible, we quickly reduce to the case of polynomials in $\mathbb{Z}[X]$ by clearing denominators. Recall that a polynomial in $\mathbb{Q}[X]$ is irreducible if and only if it is non-constant and cannot be factored as a product of two non-constant polynomials. Thus, for a non-zero $c\in \mathbb{Q}$, we see that $f(X)$ is irreducible in $\mathbb{Q}[X]$ if and only if $cf(X)$ is irreducible. Taking $c$ to be the product (or maybe the least common multiple) of the denominators of $f(X)$, we obtain a polynomial in $\mathbb{Z}[X]$.
• We defined primitive polynomial (an integer polynomial for which the GCD of the coefficients is $1$) and proved {\it our} version of Gauss's Lemma [Book 1.13]: The product of two primitive polynomials is primitive. (Sketch: $f(X) \in \mathbb{Z}[X]$ is primitive if and only if its reduction modulo $p$ is non-zero in $\mathbf F_p$ for every prime $p$. Now GL follows from the fact that $\mathbf F_p[X]$ is a domain for each $p$, and the fact that reduction mod $p$ is a homomorphism, that is, $\overline{gh} = \overline g \overline h$. We did not have time to prove the book's version of GL but will do so next week. By the way, one must interpret factors non-trivially in the book's version to mean factors as a product of two non-constant polynomials . Note, for example, that $2X^2+2$ is irreducible in $\mathbb{Q}[X]$ but not in $\mathbb{Z}[X]$. Precise definitions are important (at least to pedants like us).
• We gave examples from time to time to illustrate stuff and had a brief discussion of the binomial theorem, Freshman's Dream and characteristic $p$ [Book 1.4].

• Lecture 4:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• We proved the book's version [1.13] of Gauss's Lemma, again carefully explaining what non-trivially means. We emphasized that the book's version is really the main point, and that the version proved in Class #3, that the product of primitive polynomials is primitive, is just a tool. The key to deducing 1.13 from the version done in Class #3 is the following observation: If $f(X)$ is a primitive polynomial in $\mathbb{Z}[X]$ and $c$ is a non-zero rational number such that $cf(X) $ is also a primitive polynomial in $\mathbb{Z}[X]$, then $c= \pm1$.
• Professor Ajaya Singh came by to take a class photo. (Actually, about $2^{\aleph_1}$ photos were taken, by the time everyone's cellphone had been satisfied.)
• [Remarks 1.4] Reminder of Freshman's Dream in characteristic $p>0$, and Frobenius homomorphism.
• [Remarks 1.5] Quick review of vector spaces, linear independence, spanning, bases, dimension. If $F$ is a field, $F[X]$ is a vector space over $F$. Pointed out that $\{1,X,X^2,\dots\}$ is a basis for $F[X]$, so $F[X]$ is an infinite-dimensional vector space over $F$.
• Reminder of formal definition of GCD. We proved the long-awaited Theorem 1.8: If $R$ is a PID, (1) a GCD of two non-zero elements exists and (2) the GCD can be expressed as a linear combination of the two elements. We reminded that (3) If $R$ is Euclidean (has a degree and division algorithm. e.g., in $\mathbb{Z}$ or $F[X]$ where $F$ is a field), then repeated use of the algorithm yields the GCD and the coefficients of such a linear combination. Students were directed to the book [1.8, p. 10] for the details and encouraged to work examples (one of which occurs on Homework #2).
• [Material related to 1.6 and 1.9 in book:] Reminder [1.9.1] $F[X]$ is a PID. Reminder of result from Class #3, Euclid's Lemma 1.9.2: In a PID, if $a \mid bc$ and GCD$(a,b) =~1$, then $a\mid b$. Special case, Corollary 1.9.3: If $p$ is irreducible and $p\mid ab$, then $p\mid a$ or $p\mid b$. Note GCD$(a,b)$ is defined only up to units. In other words, if $d$ is a GCD of $a$ and $b$, and $e\in R$, then $e$ is a GCD of $a$ and $b$ if and only if there is a unit $u$ of $R$ such that $e=du$. Thus GCD$(a,b) = 1$ just means that units are the only common divisors of $a$ and $b$.
• [Related to 1.6 and 1.9 in book:] Definition of UFD; began proof of Theorem 1.9.4: If $R$ is Euclidean (has a degree and division algorithm), then $R$ is a UFD (unique factorization domain) but ran out of time. We did manage to show that every non-zero non-unit is a product of irreducibles. Proof of uniqueness is first on the agenda for Class #5. Actually every PID is a UFD (won't prove).
• We found, to our dismay, that students cannot access the notes and other handouts, which have been faithfully posted, by Nilu, on the NAP website. This resulted in a late-night email frenzy. (Apparently students can send and receive emails but cannot access the internet. Strange!)

• Lecture 5:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• We extended Corollary 1.9.3 (to Euclid's Lemma 1.9.2) to
  Corollary 1.9.3$'$: Let $R$ be a PID, $s\in\mathbb{N}$ and $p,a_1, a_2,\ldots,$ $a_s\in R$. If $p$ is irreducible and $ p \mid a_1\cdot$ $a_2\cdot\ldots\cdot$ $a_s$, then $p\mid a_i$, for some $i$.
• We used this for the proof of
  Theorem 1.9.4: If $F$ is a field then $F[X]$ is a UFD. Actually the two parts we did show that
  1. If $R$ is a Euclidean domain (Euclidean means has a degree and division algorithm , such as $\mathbb{Z}$ and $F[X]$), then every non-zero non-unit of $R$ is a finite product of irreducible elements of $R$, and
  2. If $R$ is a PID, then such a factorization is unique in the sense that, if $p_1\cdot p_2\cdot \ldots \cdot p_n$ $=$ $q_1\cdot q_2\cdot \ldots \cdot q_m$, and the $p_i, q_j$ are irreducible, then $n=m$ and there exists a re-ordering of $\{ q_1, q_2, \ldots , q_n\}$ so that each $p_i=u_iq_i$ for some unit $u_i$.
  True Theorem: Every PID is a UFD (won't prove).
• Didn't prove, PLEASE READ, related to item 1.7 p. 9:
  Proposition 1.7.0: Let $F$ be a field and $f(X)\in F[X]$. Then
  $\phantom{XXX}$ #{distinct roots of $f(X)$ in $F$} $\le$ deg $f(X)$.
• Proposition 1.18. Irreducibility mod $p$ test for $\mathbb{Z} [X]$.\quad Let $f(X)\in\mathbb{Z} [X]$:
  1. If $f(X)=$ $g(X)h(X)$, where $g(X), h(X)$ $\in$ $\mathbb{Z} [X],$ then the images in $\mathbb{F}_p[X]$ satisfy $\overline{f(X)}=$ $\overline{g(X)}\cdot \overline{h(X)}$, for every prime element $p$ of $\mathbb{Z}$.
  2. If $f(X)$ factors nontrivially in $\mathbb{Z} [X]$, then $\overline{f(X)}$ factors nontrivially in $\mathbb{F}_p$, for every $p$ with deg $f(X)=$ deg $\overline{f(X)}$, i.e. for every $p$ that does NOT divide the leading coefficient of $f(X)$.
  3. If $f(X)$ is primitive and there exists a prime element $p\in\mathbb{Z}$ such that $p$ does NOT divide the leading coefficient of $f(X)$ and $\overline{f(X)}$ is irreducible mod p, then $f(X)$ is irreducible in $\mathbb{Z}[X]$, hence also in $\Q[x]$, by Gauss' Lemma 1.13.
• Began field extensions [p. 13 of book]. Defined $E/F$, the field extension $E$ over $F$, for $F\subseteq E$, fields. Discussed $F[\alpha]$, the smallest subring of $E$ containing $F$ and $\alpha$ [p.14], and $F(\alpha),$ the smallest subfield of $E$ containing $F$ and $\alpha$ [p. 15], for $E,F$ fields and $\alpha \in E$. Considered examples $\mathbb{Q}[\sqrt 2], \mathbb{Q}(\sqrt 2), $ $\mathbb{Q}[i],\mathbb{Q}(i), $ $\mathbb{Q}[\sqrt 2][\sqrt 3] = $ $\mathbb{Q}[\sqrt 2, \sqrt 3] $. Showed $\mathbb{Q}[i]= $ $\mathbb{Q}(i)$, $\mathbb{Q}[\sqrt 2]= $ $\mathbb{Q}(\sqrt 2)$.
• Defined degree of the extension $E/F$, for $F\subseteq E$, fields, to be the vector space dimension of $E$ as an $F$-vector space. Began discussion for
  Proposition 1.20 [p. 14]: If $F\subseteq E\subseteq L$ are fields, and the degrees of $L/E$ and $E/F$ are both finite, then the degree of $L/F$ is finite and is equal to the product of the degrees of $L/E$ and $E/F$. Conversely, if the degree of $L/F$ is finite, then the degrees of $L/E$ and $E/F$ are both finite.

• Lecture 6:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• We proved Proposition 1.20: Multiplicativity of Degrees (of extension fields). We added just a couple of details to the proof in the book, which is actually rather detailed. We said (many times, and will say many times again) that one should always draw a lattice diagram (graph) showing intermediate fields at vertices, and labeling edges with degrees.
• We proved Lemma 1.23: A domain $R$ containing a field $F$ is a field if $R$ is finite dimensional as a vector space over $F$.
  This shows that $\mathbb{Q}[\sqrt2,\sqrt3]$ is a field. (Earlier we showed $\mathbb{Q}[\sqrt2,\sqrt3]$ is spanned by $\{1,\sqrt2, $ $\sqrt3,\sqrt6\}$ as a $\mathbb{Q}$-vector space.) Therefore $\mathbb{Q}[\sqrt2,\sqrt3] $ $= $ $\mathbb{Q}(\sqrt2,\sqrt3)$.
• For an element $\alpha$ of an extension field $K$ of $F$, one says that $\alpha$ is algebraic over ~$F$ provided there is a non-zero polynomial $f(X)) \in F[X]$ having $\alpha$ as a root. If no such polynomial exists, then $\alpha$ is transcendental over $F$.
• The exponential base $e$ is transcendental over $\mathbb{Q}$, and the proof is not too hard, roughly speaking, because the power series expansion of $e$ is so sparse. Also, $\pi$ is transcendental, but the proof is much harder. It is not known whether or not $\frac{e}{\pi}$ is transcendental. In fact, it's not even known whether or not $\frac{e}{\pi} \in \mathbb{Q}\,$!
• For an element $\alpha$ in a field extension $K$ of $F$, we pointed out that $F[\alpha]\cong F[X]$ if $\alpha$ is transcendental over $F$, and hence that $F[\alpha]$ is properly contained in $F(\alpha)$. If $\alpha$ is algebraic over $F$, then $F[\alpha] = F(\alpha)$, by FATSAE (below).
  We proved various characterizations of the minimal polynomial of an algebraic element:
• Proposition 1.27$\frac{1}{4}$: Let $\alpha$ be an element of a field extension $K$ of $F$ with $\alpha$ algebraic over $F$. Let $I$ be the kernel of the evaluation homomorphism $F[X] \to F[\alpha]$ taking $g(X)$ to $g(\alpha)$. Let $p(X)$ be a monic polynomial in $F[X]$. These conditions on $p(X)\in F[X]$ are equivalent:
  1. $p(\alpha) = 0$, and $p(X)$ has least degree among all non-zero polynomials $f(X)\in F[X]$ such that $f(\alpha)=0$.
  2. $I = $ $p(X)F[X] $ $=(p(X)\,)$, that is, $p(X)$ generates the ideal $I$.
  3. $p(\alpha) = 0$ and $p(X)$ is irreducible.
  Well, maybe we didn't include (c) among these conditions, but we will do so in our last class, on Thursday, 17^th May 2018.
• We proved what we call the Fundamental Theorem on Simple Algebra Extensions (FTSAE), aka Theorem 1.27$\frac{1}{2}$). It covers various things in the book (e.g., stem fields ) that seem to be a bit scattered.
• Theorem 1.27$\frac{1}{2}$ FTSAE : Let $\alpha$ be an element of an extension field $K$ of $F$. Assume $\alpha$ is algebraic over $F$, and let $p(X)$ be a monic polynomial such that (i)~$p(\alpha)=0$ and (ii) $p(X)$ has least degree among all non-zero polynomials having $\alpha$ as a root. Put $n = \deg f(X)$. Then:
  1. $p(X)$ is unique (and is called the minimal polynomial of $\alpha$ over $F$).
  2. $p(X)$ is irreducible in $F[X]$.
  3. The set $\{1,\alpha,\alpha^2 $ $,\dots,\alpha^{n-1}\}$ is a basis for $F[\alpha]$ as a vector space over $F$.
  4. For a polynomial $g(X)\in F[X]$, we have $g(\alpha)=0 $ $\iff $ $p(X)\mid g(X)$.
  5. $F[\alpha]$ is a field, and so $F[\alpha] = F(\alpha)$.
  6. $[F(\alpha):F] $ $ = n$.
• Of course item (5) follows from Lemma 1.23, but we gave another (constructive) proof, using the fact that the GCD of two gadgets is a linear combination of the gadgets. Thus one can find inverses constructively, using the Euclidean Algorithm.

• Lecture 7:
  • Module-1 Lectures
    • [1] [2] [3] [4] [5] [6] [7]
  • Modules
    • [I] [II] [III] [IV] [V]
  • go to menu
  • Notice Board
  • Exams
  • Introduction
  • Didactics
  • Lecturers
  • Students

• We finished the proof of
  Proposition 1.27$\frac{1}{4}$: Let $\alpha$ be an element of an extension field $K$ of $F$, with $\alpha$ algebraic over $F$. Let $I$ be the kernel of the evaluation homomorphism
  $\psi_\alpha: F[X] \to F[\alpha]$ by $\psi_\alpha(g(X))$ $=$ $g(\alpha)$. Let $p(X)$ be a monic polynomial in $F[X]$. These conditions on $p(X)\in F[X]$ are equivalent:
  1. $p(\alpha) = 0$ and $p(X)$ has least degree among all non-zero polynomials $f(X)\in F[X]$ such that $f(\alpha)=0$.
  2. $I =$ $p(X)F[X]$ $=$ $(p(X)\,)$, that is, $p(X)$ generates the ideal $I$.
  3. $p(\alpha) = 0$ and $p(X)$ is irreducible.
• Remark1.27$\frac{1}{3}$: Let $\alpha$ be an element of an extension field $K$ of $F$ such that $f(\alpha)=0$, for some non-zero $f(X)\in F[X]$. Then:
  1. $[F(\alpha):F]\le $degee $f(X)$.
  2. $[F(\alpha):F]$ $\le$ $[K:F]$. Note that $[K:F]$ might be $\infty$.
• Theorem 1.27$\frac{3}{4}$: Let $\alpha$ be an element of a extension field $K$ of $F$. These conditions are equivalent:
  1. $\alpha$ is algebraic.
  2. $F[\alpha]=F(\alpha)$.
  3. $F[\alpha]$ is finite-dimensional as a vector space over $F$.
• The next theorem is related to what the book calls Stem fields. Given any non-constant polynomial $g(X)$ $\in$ $F[X]$, where $F$ is any field, we can always find an extension field of $F$ in which $g(X)$ has a root. First choose an irreducible factor of $g(X)$; if we can find a root of this irreducible factor, we'll have a root of $g(X)$.
  Theorem 1.25: Construction of extension fields with roots. Let $F$ be a field and $p(X)\in F[X]$ a monic irreducible polynomial of degree $m$.
  Let $I$ $=$ $(p(X))$ $=$ $p(X)F(X)$, the ideal of $F[X]$ generated by $p(X)$. Then:
  1. $F[x]$ $=$ $\frac{F[X]}{(p(X))}$, where $x$ is the coset $X+I$, is an extension field of degree $m$ over $F$, and $p(x)=0$.
  2. If $K/F$ is a field extension, and $\alpha\in K$ satisfies $p(\alpha)=0$, then there exists a field isomorphism $\varphi$ $=$ $\varphi_\alpha :$ $F[x]$ $\overset{\cong}\to$ $F[\alpha]$ such that $\varphi(x)=\alpha$ and $\varphi(c) = c$ for each $c\in F$. Note that $\varphi((f(x)))$ $=$ $f(\alpha)$ for each $f(X)$ $\in$ $F[X]$. 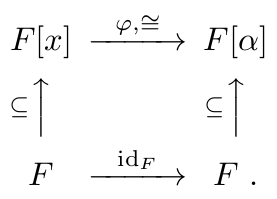Then $\varphi_\alpha$ is an $F$-isomorphism: $F[x]\overset{\cong}\to$ $F[\alpha]$.
• (We didn't do) Terminology: An $F$- homomorphism is a field homomorphism $\varphi:K\to E$, where $K/F$ and $E/F$ are field extensions and $\varphi$ is the identity homomorphism on $F$, that is, $\varphi |_F ~(=\varphi$ restricted to $F$) is id$_F:F\to F$.
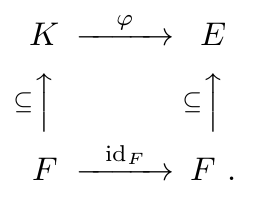
• Example 1.25.1: For the ring $R$ $=$ $\frac{F[X]}{(p(X))}$ $=$ $F[x]$ of Theorem 1.25 with $F=\mathbb{F}_2$ and $p(X)=X^2+X+1$, we have
  (a) $R$ has four elements: $R$ $=$ $\{0,1,$ $x,1+x\}$, and
  (b) $R$ is a field. We made addition and multiplication tables for $R$, using the fact that the coset $[X^2]$ $=$ $[X^2+X^2$ $+X+1]$ $=$ $[X+1]$.
• Two useful facts from ring theory: Let $R$ be a commutative ring.
  1. If $I$ is an ideal of $R$, then $\frac RI=\{$ cosets $r+I$, where $r\in R\}$ is also a ring, with inherited $+, \cdot$ from $R$.
  2. if $\psi: R\to S$ is a ring homomorphism, if $I$ is the kernel of $\psi$, and if $\pi: R \to \frac RI$ is the natural map $\pi(r)=r+I$, then there exists a one-to-one ring homomorphism $\varphi: \frac RI\to S$ such that $\varphi\circ\pi$ $=$ $\psi$. Pictorially, if we have maps $\psi$ and $\pi$ as shown, 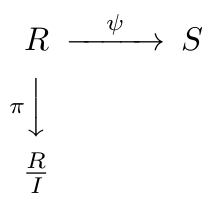then there exists a diagonal map $\varphi:$ $\frac RI\to S$ such that the diagram commutes. If, in addition, $\psi$ is a surjection (onto), then $\varphi$ is an isomorphism (one-to-one and onto).
• Corollary 1.25.2: (didn't do) If $K/F$ and $E/F$ are field extensions, $p(X)\in F[X]$ is irreducible and $\alpha\in K,\beta\in E$ satisfy $p(\alpha)$ $=0=$ $p(\beta)$, then there exists an $F$-isomorphism $\varphi:$ $F(\alpha)$ $\overset{\cong}\to$ $F(\beta)$. To prove this, just take $\varphi$ $=$ $\varphi_\beta\circ$ ${\varphi_\alpha}^{-1}$, where the isomorphisms $\varphi_\alpha$ and $\varphi_\beta$ are given by part (2) of Theorem 1.25.
  $F(\alpha)$ $=$ $F[\alpha]$ $\overset{\varphi_\alpha^{-1}}\longrightarrow$ $F[x]$ $\overset{\varphi_\beta}\longrightarrow$ $F[\beta]$ $=$ $F(\beta)$.
• Examples 1.25.3: For $F=\mathbb{R}$ and $p(X)=$ $X^2+1$, the construction in Theorem 1.25 can be thought of as creating a square-root for $-1$, or, equivalently, a root for $X^2+1$, by setting $R=$ $\frac{\mathbb{R}[X]}{(X^2+1)}$. Similarly to create a square-root for $2$, let $R=$ $\frac{\mathbb{Q}[X]}{(X^2-2)}.$
• Proposition 1.30: Let $E/F$ be a field extension. These conditions are equivalent:
  1. $E/F$ is finite, i.e. $[E:F]$ $<$ $\infty$.
  2. $E/F$ is algebraic and finitely generated over $F$, i.e. each element of $E$ is algebraic and there exists a finite set $\alpha_1,\ldots, \alpha_n\in E$ such that $E$ $=$ $F(\alpha_1,$ $\ldots,$ $\alpha_n)$.
  3. There exists a finite set of algebraic (over $F$) elements $\alpha_1,$ $\ldots,$ $\alpha_n$ $\in E$ such that $E$ $=$ $F(\alpha_1,$ $\ldots,$ $\alpha_n)$.
• Corollary 1.31: Algebraic Tower of Fields Theorem (Mentioned but didn't prove) Let $F$ $\subseteq$ $E$ $\subseteq$ $K$ be fields. If $K$ is algebraic over $E$ and $E$ is algebraic over $F$, then $K$ is algebraic over $F$.
• Discussion of roots of unity: Let $p$ be a prime number. Let $\zeta_p$ $=$ $e^{\frac{2\pi i}p}$. Then $\zeta_p$ is a primitive $p^{\text{th}}$ root of unity. In the complex plane with the $x$-axis real numbers and the $y$-axis the pure imaginary numbers, there are $p$ roots of unity, evenly spaced as $p$ points around the circle $x^2+y^2$ $=1$, including the point $x=1$, $y=0$. The minimal polynomial for $\zeta_p$ over $\mathbb{Q}$ is $p(X)$ $=$ $X^{p-1}$ $+$ $\cdots$ $+$ $X+1$.
• Lemma 1.41: If $p$ is a prime number then $p(X)$ $=$ $X^{p-1}$ $+$ $\cdots$ $+$ $X+1$ is irreducible over $\mathbb{Q}$; hence $[\mathbb{Q}(\zeta_p)$ $:$ $\mathbb{Q}]$ $=$ $p-1$.
• Exercise: Find $[\mathbb{Q}$ $(\zeta_{17}$ $,2^{\frac 15}$ $):\mathbb{Q}]$. Answer: $80$.